Крис Уоринг
Формулы на все случаи жизни. Как математика помогает выходить из сложных ситуаций

Теорема пифагора

Эта легендарная теорема (а о других вы слышали хотя бы раз?) устанавливает соотношение между сторонами прямоугольного треугольника.

Квадрат самой длинной стороны треугольника, или гипотенузы, равен сумме квадратов других более коротких сторон (они же катеты). Если известна длина обоих катетов, гипотенуза вычисляется по этой формуле:

Захотим узнать длину одной из коротких сторон – воспользуемся этой:

Раскрытие скобок

Бывает, что в уравнениях присутствуют скобки. Предположим, у нас есть некое число. Если прибавить к нему 4, а потом умножить полученную сумму на исходное число, получится 45. Все это можно представить в виде вот такого уравнения:

n × (n + 4) = 45.

Знак умножения при записи обычно опускается:

n(n + 4) = 45.

Прежде чем решить уравнение, нужно избавиться от скобок. Чтобы облегчить задачу, предлагаю представить ее в виде прямоугольника, одна сторона которого равна n метров (м), другая – n + 4 метров. Он будет выглядеть так:

Поделив длинную сторону на два отрезка, один из которых имеет длину n метров, а другой – 4 метра, получим прямоугольник и квадрат:

Теперь можем определить площадь каждой фигуры:

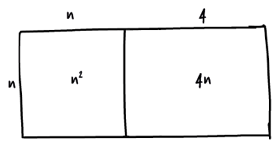
Таким образом, общая площадь прямоугольника получается равной n² + 4n, что составляет 45:

n² + 4n = 45.

Видите? Скобок больше нет! Процесс называется умножением на скобку, или ее раскрытием. Полученное квадратное уравнение решается с помощью формулы, приведенной в подразделе «Решение уравнений».

Вынесение за скобки общего множителя

Алгебраический метод, противоположный раскрытию скобок, может быть полезен при решении уравнений или преобразовании формул. Рассмотрим на примере:

4 × 3 + 5 × 3 = (4 + 5) × 3.

Проведя операции, получим:

12 + 15 = 9 × 3

27 = 27.

Равенство истинно. Истинно и то, что мы могли бы заменить тройку любым другим числом и получить: четыре раза по столько-то плюс пять раз по столько-то – это девять раз по столько-то. Если вместо «столько-то» мы возьмем букву, выражение станет алгебраическим, а задача примет такой вид:

4a + 5a = (4 + 5) a.

Обе части уравнения здесь, конечно, равны 9а. Такой процесс называется вынесением за скобки общего множителя. Можем пойти еще дальше и заменить 4 и 5 на другие неизвестные:

Xa + Ya = (X + Y)a.

Это умение – выносить общий множитель за скобки – пригодится при решении уравнений, где одно и то же неизвестное встречается несколько раз.

Надеюсь, что вышеизложенные основы помогли вам освежить воспоминания, и теперь вы готовы рассмотреть первую ситуацию. Все еще не уверены в собственных силах? Не волнуйтесь. В каждой главе мы внимательно, шаг за шагом и с подробными объяснениями разберем любую возможную проблему. Да, и никаких экзаменов. Возможно, вам это и не приходило в голову после школы, но, прочитав эту книгу, вы поймете, что на самом деле для каждого случая есть свое уравнение.

Глава 1
Прямиком из лувра

Как частный консультант по безопасности вы не имеете себе равных: ряд недавних громких дел даже привлек внимание международных СМИ. Но как только на пороге вашего офиса появляется разодетая по последней парижской моде дама, вы тут же отменяете все свои встречи и, предложив ей чай/кофе, соглашаетесь выяснить, кто из сотрудников Лувра подменяет шедевры практически идеальными копиями. Бюджет, который музей выделяет на безопасность, сильно ограничен. Вместе с заказчицей вам предстоит придумать, как при минимальном количестве охранников уберечь картины, скульптуры и прочие художественные ценности, представленные на выставке, которая недавно открылась… ну, скажем, в зале математического искусства^[2]. При этом заказчица требует, чтобы каждая часть экспозиции находилась под постоянным наблюдением хотя бы одного охранника. Как эффективно решить поставленную задачу?

Мы должны обратиться к математической логике и попытаться мыслить геометрически. Давайте начнем рассуждать о помещении и его безопасности на языке математики. Итак: обозначьте необходимое количество охранников буквой g, а затем посмотрите, получится ли уменьшить это значение. Прежде всего вам нужно разобраться в многоугольниках (полигонах).

Многоугольники – плоские фигуры с прямыми сторонами. В большинстве случаев план помещения представляет собой совокупность многоугольников, которые в основном (но не всегда, что можно увидеть на представленной ниже планировке) имеют прямые углы.

Многоугольники принято называть по количеству сторон. Треугольник представляет собой многоугольник с тремя сторонами (для полигона это число сторон является минимально возможным). Если склеить два треугольника, сторона к стороне, получится четырехсторонняя фигура, известная как четырехугольник.

Четырехугольники – прямоугольник, квадрат, трапеция, дельтоид, параллелограмм и ромб. Добавьте к двум склеенным треугольникам еще один, и образуется пятиугольник – многоугольник с пятью сторонами. Приклеивая новые и новые треугольники, вы увеличиваете количество сторон полигона.

Многоугольники бывают выпуклыми и невыпуклыми. У первых все внутренние углы меньше 180°: это означает, что, если вы смотрите на фигуру со стороны, вам кажется, будто ее стороны, как и углы, выдаются вперед, то есть являются выпуклыми. У многоугольников второй разновидности, невыпуклых, как минимум пара-тройка внутренних углов больше 180°, и появляется ощущение, что углы направлены внутрь фигуры.

Вообразите, что находитесь в комнате, план которой выглядит как выпуклый многоугольник. Где бы вы ни стояли, для обзора доступен любой угол. Если выражаться математическим языком, у вас есть возможность провести прямую от своего местоположения к каждой точке в помещении. В таком контексте линия будет означать направление обзора, а значит, для охраны любой выпуклой комнаты хватит одного человека.

К сожалению, проектировщик зала математического искусства хотел блеснуть оригинальностью или, возможно, просто увеличить площадь экспозиции, поэтому помещение приобрело вид невыпуклого многоугольника с 28 сторонами – икосиоктагона, если использовать точный термин. Точки внутри помещения, из которой можно провести прямую линию в любую часть многоугольника, не пересекая его сторон, не существует, и потому у нас есть все основания заявить: для наблюдения понадобится больше одного охранника. Итак, нам известно, что g > 1. Наверное, это и так было очевидно, однако теперь у нас появилась отправная точка.

Как уже было сказано, многоугольник можно собрать из треугольников. И, как вы, вероятно, помните со школьных времен, внутренние углы последних составляют в сумме 180°. У треугольника три угла, каждый из которых должен быть меньше 180°, а значит, эта фигура точно не является невыпуклой. Получается, что для полноценной охраны любой треугольной комнаты достаточно одного человека. (Подобное заключение, конечно, не относится к четырехугольникам или многоугольникам с количеством сторон больше трех, так как любая из этих фигур может оказаться невыпуклой.) Итак, теперь вам известно, что на каждый из треугольников, составляющих икосиоктагон, клиентке потребуется самое большее по одному охраннику. В этой связи, наверное, есть смысл упомянуть, что треугольников в многоугольнике всегда на два меньше, чем сторон: треугольник – это один треугольник (что само собой разумеется) и три стороны, четырехугольник – два треугольника и четыре стороны, пятиугольник – это три треугольника и пять сторон…

Итак, число g для комнаты с количеством стен n должно равняться по меньшей мере n – 2, что дает нам g ≤ n – 2. Если объединить это неравенство с предыдущим ограничением, получим вот что:

1 < g ≤ n – 2.

В случае с нашим залом, где по условию n = 28, диапазон возможных значений g будет представлен так:

1 < g ≤ 26.

Разбить полигональное помещение на треугольники можно следующим образом:

Разумеется, существуют и другие варианты, однако в том, что 28-сторонний полигон будет составлен из 26 треугольников, можно быть абсолютно уверенным.

Ход ваших рассуждений, кажется, устраивает клиентку, но у нее имеются вполне понятные опасения, что по залу – при достаточном бюджете – будут слоняться 26 охранников. Заверьте даму, что работа еще не закончена и что вы, приложив еще больше усилий, сумеете значительно уменьшить количество персонала.

Давайте подумаем, что получится, если распределить охранников по углам треугольников. Обозначим вершины каждого из них буквами A, B и C, причем таким образом, чтобы углы с одной и той же буквой не соседствовали друг с другом.

На иллюстрации буквы необходимо расставить в нужных местах.

«Почему это так важно?» – возможно, поинтересуетесь вы. Вот почему: выбрав вершину, обозначенную буквой А, В или С, и поместив туда соответствующего охранника, мы дадим каждой фигуре персонального наблюдателя, но некоторые из них будут обозревать больше одного треугольника. Дело в том, что некоторые углы относятся сразу к нескольким треугольникам. Разбивая помещение на простейшие выпуклые многоугольники, мы стремились, чтобы общими вершинами – особенно в двух углах зала, обведенных кружками, – обладало как можно большее количество треугольников. Таким образом, если у многоугольника n вершин, то количество углов, обозначенных как A, B или C, должно быть около n ÷ 3. Поскольку n ÷ 3 не обязательно будет целым числом, нам придется округлять его в меньшую сторону. В зависимости от точной формы помещения могут найтись способы, как еще уменьшить количество персонала, но будьте уверены: полученный ранее результат окажется верхней границей минимального числа охранников. Итак, теперь вы знаете:

Такие полускобки означают округление в меньшую сторону. В нашей ситуации число охранников будет подсчитываться так:

Это означает: независимо от конфигурации помещения с 28 сторонами для его охраны понадобится не более восьми человек. Клиентку это, кажется, радует – ведь количество персонала уменьшилось более чем втрое. Но можно ли улучшить результат?

А теперь вам придется пойти опытным путем и выявить те закономерности, что помогут улучшить промежуточный результат. Нет никакой гарантии, что эвристический подход поможет оптимизировать предыдущее решение, но клиентка совершенно точно обрадуется, если охранников в зале станет еще меньше.

Элегантное доказательство

Теорема картинной галереи была доказана канадским математиком чешского происхождения Вацлавом Хваталом еще в 1970-х годах, а потом упрощена американским профессором Стивом Фиском. В этой главе приводится более простая, вторая версия. Математики называют это доказательство (оно приснилось Фиску, задремавшему в автобусе) «элегантным» – то есть простым и понятным даже неспециалисту решением сложной проблемы. По этой причине предложенные американцем рассуждения были включены в «Доказательства из Книги»^[3] – сборник самых красивых и глубоких теорем из различных областей математики, составленный Мартином Айгнером и Гюнтером Циглером.

Вы замечаете, что на плане есть несколько мест с наилучшим обзором. Например, из точки на иллюстрации ниже зал просматривается почти полностью (за исключением заштрихованных областей):

Следующего охранника вы помещаете таким образом, чтобы слепые пятна оказались в его поле зрения. Большинство нужных областей он увидит из этой точки:

За неохваченной крошечной зоной – она находится в нижнем левом углу – сможет наблюдать третий охранник.

Клиентка, которая выглядит приятно удивленной как простотой ваших рассуждений, так и экономией на охране, тянется к своей сумке Louis Vuitton – хочет выплатить гонорар.

– Не стоит, мадам, – останавливаете вы даму. – Я с радостью откажусь от денег в обмен на пожизненный абонемент в Лувр и индивидуальную экскурсию по залу математического искусства.

– Конечно, мсье, – подсчитывая в уме расходы на троих охранников, соглашается она.

Очевидно, прежде чем совершить экскурсию, вам придется дождаться поимки преступника.

Сомнительный бизнес

Воровство и фальсификация произведений искусства были и остаются доходным делом. Даже Микеланджело начинал с копий – правда, по сравнению с некоторыми знаменитыми мастерами преступных дел он выглядит полным дилетантом. Так, британская семья Гринхолш с 1989 по 2006 год заработала миллион фунтов стерлингов, продавая подделки, сработанные в сарайчике на собственном заднем дворе. Шон Гринхолш, владеющий сразу несколькими художественными манерами, умелый скульптор и металлообработчик, был признан самым разносторонним фальсификатором. Будучи самоучкой, Шон изготовил по меньшей мере 120 подделок. Гринхолши попались в 2006 году, но не из-за того, что эксперт распознал фальшивку: просто Шон Гринхолш допустил ошибки в клинописи на барельефе. Француз Стефан Брайтвизер, путешествуя по Европе, сумел с 1995 по 2001 год украсть из небольших музеев и галерей более 250 произведений искусства. Пока его подруга следила, не идет ли охрана, он вынимал картины из рам. Продавать украденные полотна мужчина даже не пытался. Когда Брайтвизера арестовали после кражи 500-летнего горна из швейцарского музея, его мать, к сожалению, уничтожила многие похищенные работы. В 1990 году группой злоумышленников из Бостонского музея изящных искусств были украдены художественные произведения на сумму 500 миллионов долларов. Ни одна из картин до сих пор не обнаружена (а это полотна Вермеера, Дега, Рембрандта и Мане), преступники тоже не найдены, а вознаграждение в размере 10 миллионов долларов так никому и не выплачено.